The Spreadsheet
This is a fairly simple Excel spreadsheet; I have "protected" the bits that contain text and calculated values against inadvertent modification, and the values to be entered by the user are highlighted in red. You can download the spreadsheet by clicking this link. All length measurements used in the spreadsheet are in millimetres.
The first few lines define the variable names, using the same letters/mnemonics as in Riccardo's text where appropriate.
The first "tool" at lines 12 through 14 allows the user to determine the reproduction ratio of a lens when focused at its close focus distance. Set the lens to its closest focus distance and place a ruler or tape measure horizontally at that distance from the camera, focusing on the ruler by moving the camera (or the ruler) but not disturbing the setting of the lens's focusing ring. By viewing the ruler through the viewfinder, determine how many milimeters of the ruler are visible left-to-right across the viewfinder, and use that value to overwrite the red numbers in the cel under the column marked "X". For a more accurate measurement, take a photo of the ruler and read off the length from the neg/transparency, or from the digital image; this will remove the error caused by the fact that many SLR viewfinders do not actually show the whole of the area of image. Two values of R are shown; the first is for a 35mm SLR body, the second for the smaller DX-sized sensor found in Nikon SLRs.
The second tool at lines 16 through 19 allows the user to estimate the effective focal length of a lens when focused at a given distance, assuming that the reproduction ratio at that distance is known (which can be calculated as described above if not known). The relevance of this is that many modern lenses change their effective focal length as they focus on closer objects; this is particularly true of lenses that employ "internal focusing" techniques - the reduction of focal length in effect results in a corresponding increase in the extension of the lens, hence allowing it to focus closer without extending the physical length of the lens. With lenses like this, using the focal length of the lens quoted by the maker, calculated when the lens is focused on infinity, will be a poor basis for predicting what happens at the lens's closest focus distance when you add an extension tube or supplementary lens. The initial values in the spreadsheet are for the 200mm Nikkor AF macro lens; as can be seen, this lens behaves more like a 125mm lens at its closest (R=1) focus setting. This tool also calculates effective values of t (the image-to-lens distance) and the effective extension (ext) at this setting.
The third tool at lines 21-23 shows how the image-to-lens distance (t) and the lens focal length (F) affect the reproduction ratio (R). At 1:1, t is twice the focal length of the lens (and the overall focusing distance, D, is four times the focal length of the lens).
The fourth tool, lines 25-27, shows how much extension is needed to get a given reproduction ratio. Note that you have to take account of any extension already included by the focusing mechanism of the lens if the lens's focus ring is not on infinity; for example, the initial values in the spreadsheet show that the 200mm AF Nikkor, which has an effective F of 125mm at its 1:1 setting, will need a total extension of 250mm to get t 2:1. However, as it already effectively has an extension of 125 at that setting (see line 19), then an additional 125mm of tubes will get you to 2:1.
29-31 show the change in overal focus distance, D, as you vary F and R. If you keep F constant and change R, it neatly shows that the minimum focus distance is 4 times F, and is achieved when the reproduction ratio is 1 (life size); as you increase magnification past 1, D increases, but the working distance will decrease.
33-35 is a handy calculator to determine the working distance (WD), given D and the physical length of the lens. This is a trivial calculation; it simply subtract the lens length and the depth of the camera body (bayonet to film/sensor, which is 46.5mm for a Nikon SLR) from D.
37-39 and 41-43 calculate a focal length from a supplementary lens's strength (usually expressed as a diopter value), and vice-versa. A 1 diopter lens has a focal length of 1000mm (1000/1); a 2-diopter lens has a focal length of 500mm (1000/2), etc. The Nikon diopter lenses come in 1.5 diopter (3T, 5T) or 2.9 diopter (4T, 6T); the Canon 500D is a 2 diopter lens. "Prime" lenses are often used in the reverse position as supplementary "diopter" lenses; a 50mm prime is a 20 diopter lens.
45-47 shows the effective overall focal length when you add a supplementary lens to a lens of a given focal length. As can be seen, adding a supplementary lens has the effect of reducing the effective focal length of the macro lens.
The remainder of the spreadsheet, 49 through 70, gives a means of determining, for a given lens, what the effect of adding combinations of extension tubes and/or supplementary lenses will be. In the red boxes on line 55, you feed in the focal length of the lens at infinity (F), the reproduction ratio at the lens's closest focus (Max R), the focus distance (D) at Max R, the length of the lens when focused on infinity (L at infinity), and the length of the lens when focused at D (L at Max R). Column C can be used to add extension tubes; you simply fill in the number of tubes of a given length added, so if you want to add two PK-12 tubes, write "2" in cell C63 and leave the others zero. The "other" row allows a non-standard tube, or the length of a bellows, to be specified. "Total ext" shows how much extension you have added. Similarly for diopter lenses - there are handy cells to specify the Nikon and Canon lenses, plus three prime lens focal lengths that are often used reversed; you again have the "other" cell to specify something else altogether. Diopter values are additive; the strength of two 1.5 diopter lenses is 3 diopters.
Having filled in the necessary numbers, the calculated values show the overall focal length when the lens is focused at infinity (Max OFL) and at its closest point (Min OFL), the min and max values of R that can be expected, the focus distances at min and max R, and the working distances at min and max R. For example, if you add a 6T to a 200mm Nikkor, you should expect to get magnification values in the range 0.6 to 1.7.
As I have said, these calculations will only serve as an approximation to the actual behaviour of a real lens; however, they are hopefully useful in getting a "feel" for the effect of different combinations.
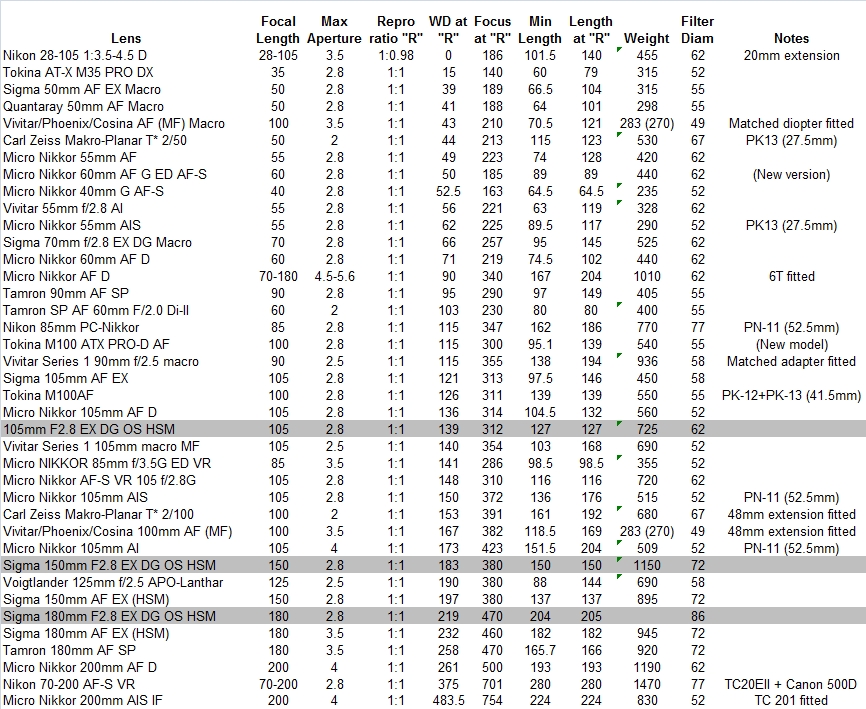
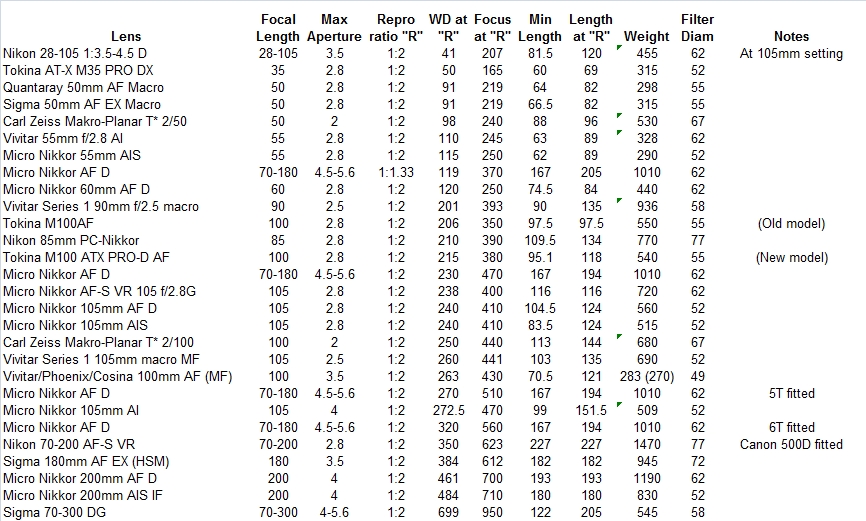
The following tables give some practical data on the behaviour of some of the popular macro lenses that are available in Nikon bayonet fit, derived from various web sources and manufacturers' data. The first table shows working distances for lenses at 1:1; where the addition of a tube, a diopter, or a teleconverter is needed to get to 1:1 this is indicated in the Notes column. The second table shows data for 1:2 reproduction ratio (R=0.5) where that was available to me. The third table shows data for a reproduction ratio of 1:1.5; this is potentially useful for practical comparison between the behaviour of a lens on a DX body relative to its behaviour on FX, as a subject that fills the DX frame at 1:1.5 will fill the FX frame at 1:1.
If you have data on other macro lenses that are available in Nikon bayonet fit, or have corrections to what I have shown here, please send me an email so that I can update the table.
Rows shaded in grey are recent additions/changes to the tables.